​​​​​Примеры решения заданий Дистанционной Акмуллинской олимпиады БГПУ имени М.Акмуллы

1.Сумма шести последовательных чисел равна 1275. Найти эти числа.

Решение: Пусть 1 число Х, то2 число будет (х+1), 3 число (х+2), 4 число (х+3), 5 число (х+4), а 6 число (х+5). Зная, что сумма этих чисел равна 1275. Составим уравнение:

Х+(х+1)+(х+2)+(х+3)+(х+4)+(х+6)=1275

6х+15=1275

6х=1275-15

6х=1260

Х=1260:6

Х=210

Ответ: 210, 211, 212, 213, 214, 215, 216.

 2. Восстановите математическую запись примера:

    AHHA

+  BAЛЯ

   4 8 0 9

Здесь разные буквы обозначают разные цифры, а одинаковые буквы – одинаковые цифры.

Решение:

А+Я=9                     Н+А=7                    

Н+Л=0                     А+В=4

Значит А не больше 3.

Если подставить вместо А-1, а вместо Н-6 получится: 4809-1661=3148.

Ответ:АННА=1661, ВАЛЯ=3148

Модуль 1. Кратко о математических олимпиадах

Целесообразно начинать подготовку «олимпиадников» в 5-7 классах. Только при таком подходе, учащийся, попавший на олимпиаду в 8-9 классах, будет чувствовать себя уверенно: скажется опыт решения нестандартных задач, накопленный за несколько лет. Начиная свою работу с одарёнными детьми, всегда знакомлю их с основными, важными моментами, на которые нужно обратить внимание при решении олимпиадных задач. Для себя составила Памятку по решению олимпиадных задач, включающую в себя несколько основных пунктов.

1.  Внимательно прочитайте условие задачи. Проверьте условие задачи на правдоподобность.

2.  При решении задачи должны быть рассмотрены все возможные варианты постановки задачи.

3. Необходима проверка правдоподобности полученных результатов. После написания олимпиадной работы внимательно ее прочитайте. Автору приходилось из ответов узнавать о том, что существуют мухи, летающие со скоростью до 200 км/час; существует многоугольник, одновременно являющийся и выпуклым, и вогнутым, и т. д.

Из истории олимпиады.

Всем людям свойственно соперничество, поэтому многим важно признание не только ближайшего окружения, но и конкурентов. Для того чтобы выяснить, кто же самый умный еще в эпоху Ренессанса организовывались всевозможные интеллектуальные соревнования. Основным предметом, где взрослые профессионалы соревновались за звание самого умного, была математика. Официально самой первой олимпиадой, считается олимпиада, по математике, проведенная в 1934 году Ленинградским университетом. Именно она положила начало олимпийскому движению на территории бывшего Союза. Спустя всего год, уже в 1935 году математическая олимпиада приобрела большое число участников, где наравне со студентами, пробовали свои силы 122 школьника....

Математическая олимпиада – это заключительный этап внеурочной и урочной работы по математике.

В мире математические олимпиады – самые престижные. Страны, для которых национальные интересы престижны везде, уделяют олимпиадному движению огромное внимание. Китайцы, победители нескольких последних международных математических олимпиад в командном зачете, сборную готовят целый год и создают все условия для успешной работы. В России пока похуже, но благодаря отдельным людям и организациям, ведется очень активная работа и уже есть весомые успехи – это победа нашей сборной в 48-ой Международной математической олимпиаде.

Модуль 2. Всероссийская олимпиада школьников по математике. ШКОЛЬНЫЙ ЭТАП .

1. В ящике 25 кг гвоздей. Как с помощью чашечных весов и одной гири в 1кг за два взвешивания отмерить 19 кг гвоздей?

2. Поставьте вместо звездочек в выражение * + ** + *** + **** = 3330 десять различных цифр так, чтобы получилось верное равенство.

3. В магазине картофель расфасовали в 24 пакета по 3 кг и 5 кг. Масса всех 5-килограммовых пакетов равна общей массе 3-килограммовых. Сколько было 3- и 5-килограммовых пакетов?

4. Примере a ∙ b + c ∙ d + e ∙ f , a увеличили на 20%, b уменьшили на 20%, c увеличили на 60%, d уменьшили на 40%, e увеличили на 50%, f уменьшили на 36%. После этого пример решили и получили 80. Найти a ∙ b + c ∙ d + e ∙ f.

Решения заданий ВОШ школьного этапа

Небольшая передышка.... Проверим вашу способность мыслить логически

Как проверяли логику у разведчиков

Перед вами рисунок вымышленной местности. Ниже следуют вопросы, ответы на которые можно найти, внимательно рассмотрев этот рисунок – в нём сокрыто множество подсказок! Попробуйте ответить на них, не заглядывая в ответы!

Вот эти вопросы:

1. Много ли времени осталось до новолуния?
2. Скоро ли наступит ночь?
3. Какое время года на рисунке?
4. В какую сторону течет река?
5. Судоходна ли она?
6. С какой скоростью движется поезд?
7. Давно ли прошел здесь предыдущий поезд?
8. Долго ли будет двигаться машина вдоль железной дороги?
9. К чему должен подготовиться водитель?
10. Есть ли здесь поблизости мост?
11. Есть ли в этом районе аэродром?
12. Легко ли машинистам встречных поездов тормозить состав?
13. Дует ли ветер?

• ОТВЕТЫ на них

• Небольшая передышка

  

Онлайн-ТЕСТ

Модуль 3. ОНЛАЙН-тест

Модуль 4. Типовые задания муниципального этапа олимпиады по математике для 7 классов

1. В двузначном числе A поменяли цифры местами и получили число B . Найдите такое A , чтобы сумма A+ B делилась на 17.

2. За круглый стол сели 12 человек, некоторые из них – рыцари, а остальные – лжецы (рыцари всегда говорят правду, а лжецы всегда лгут). Затем каждый из них сказал: 18 «Среди моих соседей есть лжец». Какое наибольшее число из сидящих за столом может сказать: «Среди моих соседей есть рыцарь»?

3. Петя купил одно пирожное, два кекса и три бублика, Аня купила три пирожных и бублик, а Коля купил шесть кексов. Все они заплатили за покупки одинаковые суммы денег. Лена купила два пирожных и два бублика. А сколько кексов она могла бы купить на ту же потраченную ей сумму?

Решения заданий муниципального (районного) этапа

Решения типовых заданий "Турнир Архимеда. Математическая регата." г. Москва

1.     Говядина без костей стоит 90 рублей за килограмм, говядина с костями — 78 рублей за килограмм, а кости без говядины — 15 рублей за килограмм. Сколько костей в килограмме говядины?

2.   Дан бесконечный ряд чисел:   2, 6, 12, 20, 30, 42...

Укажите закономерность и найдите число, стоящее на 2003-м месте.

3.   У трех членов жюри спросили: «Сколько команд будет участвовать в математической регате?» Один сказал: «Меньше семидесяти двух». Другой: «Меньше семидесяти одной», — а третий: «Меньше семидесяти трех». Сколько команд участвовало в регате, если правы были в точности двое членов жюри?

Решение типовых заданий Международного математического турнира городов .г. Москва

Задача 1. Автобусы из Москвы в Орёл выходят в начале каждого часа (в 00 минут). Автобусы из Орла в Москву выходят в середине каждого часа (в 30 минут). Поездка между городами занимает 5 часов. Сколько автобусов из Орла встре- тит автобус, вышедший из Москвы, на своем пути?

Задача 2. Три щедрых друга, у каждого из которых есть конфеты, перераспределяют их следующим образом: Вася отдает часть своих конфет Пете и Коле, отчего количества конфет у них удваиваются. После этого Петя отдает часть сво- их конфет Коле и Васе, отчего количества конфет у них тоже удваиваются. Наконец, Коля отдает часть своих конфет Васе и Пете, у которых опять же количества удваиваются. Оказалось, что у Коли и в начале, и в конце было 36 конфет. Сколько всего конфет у мальчиков?

Решения, ответы

Решение, ответы заданий "Турнир Архимеда. Математическая регата." г. Москва

Модуль 5. Домашняя олимпиада

Домашняя олимпиадаЗадание

1. Квадрат числа состоит из цифр 0, 2, 3, 5. Найти его. 

2. На часах половина девятого. Чему равен угол между часовой и минутной стрелками?

3. Каждый из трех приятелей Тимур, Артур и Булат либо всегда говорит правду, либо всегда лжет. Всем троим задали вопрос: «Есть ли среди двух остальных хоть один правдивый?». На это Тимур ответил: «Да». Артур ответил: «Нет». Что сказал Булат? ( Слово приятеля в данном случае означает, что каждый из троих знает об остальных, кто прав, а кто лжец).

Конкурс по решению головоломок

Скрыто от студентов:СтраницаРешение головоломки

Модуль 6. Решение комбинаторных задач

Решение комбинаторных задач с помощью построения специальной схемы – дерева возможных вариантов и правила умножения.

Задание 1

Артур, Бари и Василь купили три билета на 1-е, 2-е и 3-е места первого ряда на футбольный матч. Сколькими способами они могут занять имеющиеся места?

Решение (с помощью дерева вариантов).

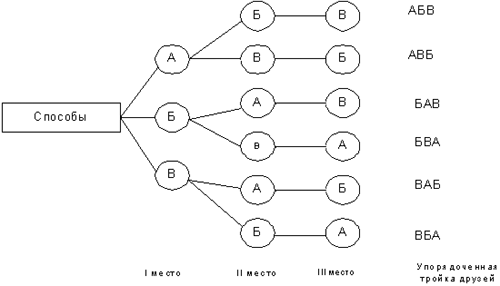
Ответ: 6.

Решение (с помощью правила умножения). На 1-е место может сесть любой из трёх друзей, на 2-е – любой из двух оставшихся, а на 3-е – последний. По правилу умножения у троих ребят существует 3*2*1 = 6 способов занять имеющиеся места

1. Модуль 7. На досуге

   Упражнение СВЕТАФОР

     Развиваем внимание 

   Упражнение  " Светофор"  Ваша задача – как можно быстрее произнести вслух название цвета букв слов, что написаны на этой картинке. Например, читаем синий, зеленый черный и т.д. Будьте очень внимательны – не путайте слова и цвета их букв. При этом работают оба полушария. Левое полушарие “читает“, а правое отслеживает цвет.

   

История возникновения нуля

• ЭТО интересно!

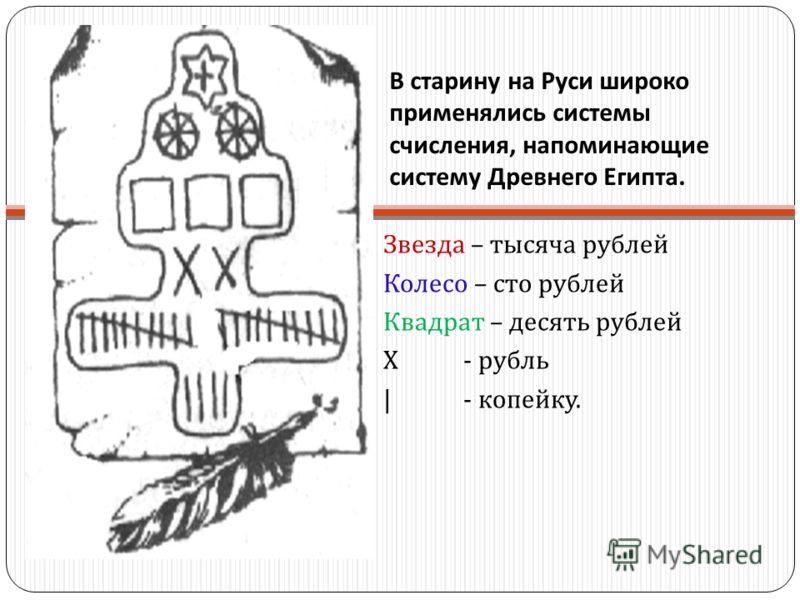
  В старину на Руси число 1232 руб. 4 коп. писали так:

  

• Разгадывание ребуса

  ОТВЕТ ребуса